¿Qué relación hay entre los taxis y la Segunda Guerra Mundial?
Lunes. 10 de septiembre de 1942. 11:23 de la mañana. 5 minutos arriba, 5 minutos abajo. Peter y Ellen, dos ingleses, de los de judías naranjas para desayunar, salen a comer a su banco de siempre de Bletchley Park.
“Peter”
“Dime, Ellen”
“Ese taxi… ¿no pasó ayer por aquí a esta hora?”
“¿Eh?”
“Sí, el taxi que está parado en el lado izquierdo de la calzada (porque es el lado natural si llevas un carro de caballos y no somos bárbaros como los franceses), ¿no pasó ayer por aquí? ¿No te resulta extraño?
“Para que fuese raro necesitaríamos saber cuantas veces sucede y la cantidad total de taxis que hay en la ciudad, para ser capaces de calcular lo “raro” que es ver ese taxi dos veces seguidas”
“¿Cuántos taxis habrá en la ciudad, Peter?”
Nunca una pregunta tan estúpida ayudó tanto en la victoria de una guerra. Vamos a ello.
Tras la pregunta de Ellen, Peter se da cuenta de que cada taxi lleva siempre visible su número de licencia en el exterior.

Ambos deciden quedarse sentados en el banco e ir apuntando los taxis que van pasando: consiguen, tras un par de horas, apuntar un número total de taxis distintos que llamaremos m , del total de taxis, que llamaremos N. Para facilitar el trabajo deciden ordenarlos (ver nota 1 al final) de menor a mayor número de licencia (llamaremos X1 a la licencia menor, X2al siguiente, así hasta llegar a Xm ).
Pero ni Peter ni Ellen saben el número total (N) de taxis. ¿Se puede conocer este número a partir de los taxis observados Spoiler: sí.
¿Qué sabemos?
Tenemos apuntado en nuestra libreta números de licencia ordenadas, donde X1 es la menor y Xm la mayor. La primera observación que podemos hacer es que, lógicamente, N probablemente será mayor que Xm : el número total de taxis siempre va a ser mayor o igual que la licencia más alta observada. ¿Cuánto es de probable? Si hay N=1.000 taxis en la ciudad y hemos apuntado taxis, la probabilidad es tan solo del 10% (ver nota 2 al final para más detalles). Por tanto, lo normal es que la licencia más alta sea menor que N , por lo que el número estimado de taxis de toda la ciudad (llamaremos N ̂ al estimador) ha de ser algo mayor que Xm , es decir Xm, multiplicado por alguna cantidad que lo haga más grande. Expresado matemáticamente, una idea podría ser la siguiente:

Esta fórmula nos dice que, según vamos apuntando cada vez más taxis (es decir, m va creciendo y Xm probablemente también lo haga), el número (m+1)/m va siendo cada vez más pequeño. ¿Qué sucedería si pudiésemos apuntar todos los taxis?
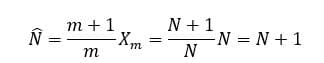
¡Maldición! Lo que significa la fórmula de arriba es que, aun apuntando todos los taxis, nuestra estimación siempre será deficiente: en estadística, todo estimador que merezca la pena debería cumplir que, si estuviera en nuestra mano poder medir todo lo medible, el estimador y el valor real deberían coincidir. ¿Cómo lo solucionamos? Simple. Restándole ese exceso de una unidad. El estimador del número total de taxis de una ciudad quedaría así:

Obviamente la construcción anterior es solamente la idea intuitiva y lógica de lo que tendría que salir y que, oh bendita matemática, se demuestra que coincide con la expresión real del estimador cuando este es derivado de forma rigurosa. Puedes ver [2] para más detalles o puedes mandarme un mail a alvarezljavier@uniovi.es.
¡Basta de teoría! Veamos un ejemplo práctico, que contó el gran Juan Antonio Cuesta en la charla que dio con motivo del día Pi en Naukas. Juan se dedicó toda una mañana a sentarse en un banco de Bilbao, llegando a apuntar hasta m=48 taxis, siendo el número total de licencias de la ciudad N=774 .
| m (nº taxis apuntados) | Xm(máximo apuntado) | (N ̂ estimador) | Intervalo de confianza | Longitud intervalo |
| 5 | 662 | 794 | (662, 1205) | 543 |
| 10 | 703 | 773 | (703, 948) | 245 |
| 20 | 761 | 799 | (761, 884) | 123 |
| 48 | 761 | 777 | (761, 810) | 49 |
Como se observa en la tabla, cuando solo tenía apuntados 5 taxis, la estimación era muy deficiente, y va acercándose al valor real (siempre por encima por el tipo de estimador que hemos decidido construir). ¿Por qué? La estadística se alimenta de datos: pocos datos, mal resultado. Como habrás advertido, hay dos columnas nuevas en la tabla. La primera es lo que llamamos en estadística intervalo de confianza: dos números entre los cuales estará el valor desconocido con cierta probabilidad (95% en el caso de la tabla anterior), ya que la estimación puntual puede ser bastante imprecisa y muy dependiente de la suerte que tengamos al apuntar. Puedes ver la expresión explícita del intervalo en la nota 3 al final de esta entrada. La segunda columna no es más que la longitud de dicho intervalo, que vemos como se va reduciendo linealmente: si medimos el doble de taxis, la longitud se reduce aproximadamente a la mitad, algo excepcional en estadística, ya que el error no suele depender linealmente del tamaño de datos que apuntamos.
En la imagen inferior puedes ver como evolucionaría esa estimación puntual (línea azul) según vamos apuntando cada vez más taxis, y cómo evolucionan distintos intervalos de confianza (IC). Os dejo el código en R (software estadístico) para quien quiera juguetear con estas estimaciones.
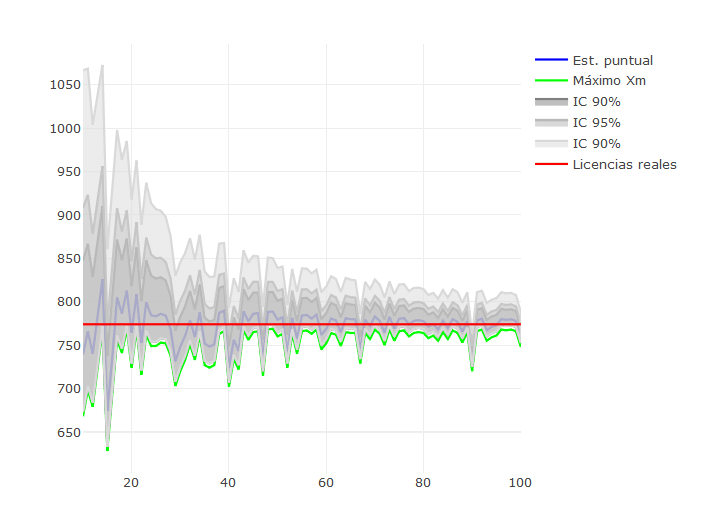
Gráfica generada con el código R anteriormente enlazado. La línea roja horizontal representa las licencias reales de Bilbao (el número N que queremos estimar). El eje horizontal representa los taxis que vamos apuntando en nuestro banco. La línea verde representa la licencia más alta ( Xm) que vamos observando (nótese que para cada caso – cada valor del eje horizontal- los valores son simulados. La línea azul representa el estimador N ̂ : como es lógico, según aumentamos los taxis que medimos, a línea azul se va pegando a la línea roja. Las bandas grises representan diferentes intervalos de confianza (IC): bandas entre las cuales podemos decir que el número total de taxis N caen dentro de dicha banda con cierta probabilidad.
Meh, se te ha quedado el cuerpo, así como de domingo de resaca, ¿verdad? Tú venías buscando alguna genialidad para desencriptar mensajes nazis y te has encontrado con dos ingleses contando taxis. ¿Qué tiene que ver esto con la Segunda Guerra Mundial?
Aunque no soy historiador (ni lo pretendo), si tuviese que hablar de uno de los hechos diferenciales entre la Primera Guerra Mundial y la Segunda Guerra Mundial sería la importancia de la ciencia. Muchas son las películas y documentales que se han hecho sobre la importancia que tuvo la criptografía y el primer computador mecánico, creado con las ideas de Ada Lovelace (que nunca se la nombra) y Alan Turing. Pero hubo un hecho diferencial aún más importante a mi parecer y es el uso de la publicidad bélica: una de las (múltiples) razones por la que los nazis consiguieron resistir tanto tiempo fue por su espléndida estrategia de propaganda, su capacidad para parecer mucho más grande e invencible de lo que era en realidad.
Corrían los años 1942-1943, y aunque eran bastante menos en número y capacidad económica, la imagen que se tenía era que los alemanes y sus partidarios eran imparables y que su capacidad militar era imbatible. Los Aliados (EE.UU., Reino Unido, Francia los días impares, etc.) no terminaban de reducir al bando nazi y, sobre todo, habían perdido el relato de la guerra (mucho más importante a veces que ganar la guerra, que se lo digan a la pobre URSS), por lo que la sensación y el ánimo, tanto de las tropas como de la población, era de absoluta derrota. Dado que la maquinaria de propaganda alemana se afanaba en hacer gala de su supuesta capacidad militar, el principal objetivo de los servicios de inteligencia aliados era, amén de ser capaces de optimizar recursos humanos y económicos, el de ser capaces de cuantificar cuáles eran los verdaderos recursos y efectivos militares con los que contaba Hitler.
¿Cómo iban a atacar un territorio, sin saber si tenían posibilidades de ganar? ¿Cómo iban a poner en juego vidas, dinero y maquinaria militar sin tener la certeza de que la correlación de fuerzas estaba de su lado?
Antes estas dudas, fueron muchos los meses en los que los Aliados asumían una derrota en cada batalla y no libraban otras tantas. A finales de 1942 e inicios de 1943, la unidad de inteligencia llamada “Economic Warfare Division of the American Embassy” se percató de que la metodología con que las unidades de inteligencia estaban intentando ganar una guerra del siglo XX eran propias del siglo XIX. Entre otros tantos errores, los modelos de estimación que estaban usando para cuantificar el potencial militar alemán eran muy poco precisos, basados en interrogatorios y rumores, lo que hizo que la maquinaria alemana pareciese un monstruo mucho más grande de lo que era en realidad. Ingleses y americanos habían sido capaces de mejorar técnicamente los (tanques) Panzer alemanes pero estaban atemorizados por la capacidad militar que Alemania decía estar desarrollando con su nuevo modelo Panzer V. En concreto, la inteligencia aliada estaba muy interesada en conocer la capacidad de producción de dichos tanques y llantas de neumáticos que Alemania era capaz de producir en un periodo de tiempo, ya que habían observado que dichos tanques eran muy pesados (por el blindaje que llevaban) y sospechaban que Alemania tardaría bastante tiempo en producir cada unidad.
¿Y si pudiesen realizar una estimación “aceptable”? En ese caso, podrían ser capaces de trazar una estrategia conjunta (como así hicieron en la Conferencia de Casablanca en 1943, con algunas de estas estimaciones) para decidir dónde atacar, con qué frecuencia debían realizar los ataques y que respuesta podían esperar de los alemanes.
¿Cómo realizar la estimación del total de los tanques alemanes?
De la misma forma que hemos podido estimar el número de taxis. He aquí donde nuestros jubilados ingleses entran en juego. Gracias a que los alemanes son alemanes, los tanques que producían llevaban todos un número de lote. Una numeración que servía a los alemanes para mantener su cuadriculado orden, pero que también permitió a los aliados recopilar una colección de números de serie (el equivalente a la licencia de taxi), tanto en operaciones de espionaje (tenían hasta “libros de contabilidad” con el inventario de los tanques) como en los tanques que eran capturados en batalla o derrotados. El proceso detallado de como los alemanes marcaban sus tanques (así como las llantas de neumático) pueden verse en el artículo referido en [3].


Distribución de los números de serie de los tanques Panzer I, II, III y IV. Gráfica y tabla extraída de [3].

| Fecha | Estimación “tipo taxi” | Estimación anterior de la inteligencia aliada | Registro real |
| Junio 1940 | 169 | 1000 | 122 |
| Junio 1941 | 244 | 1550 | 271 |
| Agosto 1942 | 327 | 1550 | 342 |
Como vemos en la tabla, en junio de 1940 las inteligencias norteamericanas e inglesas creían que los alemanes habían fabricado 1000 tanques. Esa cantidad, sumada a las que pensaban que habían fabricado en junio de 1941 y en agosto de 1942, hacían pensar a los aliados en la capacidad indestructible del ya por aquel entonces III Reich. La estimación estadística hizo que se tuviese una estimación mucho más precisa como luego se pudo comprobar al incautar los documentos oficiales de las fábricas alemanas. Fueron estas estimaciones las que permitieron saber en febrero de 1944 (ver [3]), meses antes del famoso Desembarco de Normandía, la cantidad de tanques Panzer V que los alemanes iban a movilizar hasta aquella zona. Gracias a una simple fórmula, gracias a un simple conteo de taxis, supieron que Hitler podía ser derrotado.
Y ya sabe que las guerras del siglo XXI ya no son militares sino comerciales: usando los números IMEI de los teléfonos, las compañías de la competencia son capaces de estimar la cantidad de móviles iPhone que son capaces de producir y vender.
Quién se lo hubiese dicho a Peter y Ellen.
Notas técnicas:
1. Para que la metodología tenga sentido, se deben realizar algunas suposiciones previas. La primera: las licencias se otorgarán (como así sucede en la realidad) de forma correlativa, sin saltarse ningún número. La segunda hipótesis: cada taxi tiene la misma probabilidad de aparecer, algo que no es estrictamente cierto en la realidad. Y la tercera hipótesis en realidad es una autorización: permitimos que los taxis puedan salir repetidos.
2. Como nos enseñaron de pequeños, la probabilidad de que algo suceda se puede calcular aplicando la regla de Laplace (siempre que los sucesos sean equiprobables, como hemos asumido en la nota técnica anterior), tal que la probabilidad de un evento será el número de casos favorables entre el número de casos posibles. ¿Qué significaría que el valor más alto apuntado coincida con el valor N? ¿Cuántos casos tengo favorables? Una vez eliminado ese taxi, de los N-1 taxis disponibles en la flota, observaré m-1 de ellos, de forma que tengo calcular de cuantas maneras puedo elegir N-1 taxis agrupándolos en grupos de m-1 taxis (sin darle importancia al orden en el que van apareciendo). El número de maneras viene dado por lo que se conoce como número combinatorio ((N-1)¦(m-1)) cuya fórmula es (n¦k)=n!/k!(n-k)!, siendo n! el factorial de dicho número. ¿Cuáles serían los casos posibles? De entre todos los taxis que tengo, tendré que averiguar cuantos grupos de taxis puedo formar (sin importar el orden de nuevo), siendo (N¦m). . Reduciendo las fracciones nos queda finalmente que la probabilidad buscada es justo
![]()
3. Un intervalo de confianza está formado por dos valores entre los cuales podamos decir que, de cada 100 ciudades donde yo vaya a contar taxis, el valor N caiga dentro de ese intervalo casi siempre. ¿Qué significa “casi siempre”? Obviamente debemos permitir cierto error (en este caso, una incertidumbre o error del ? = 5%), ya que la única forma de conseguir un intervalo en el que tengamos la absoluta certeza de que nuestro valor va a estar dentro es el intervalo formado por todos los (infinitos) números positivos. Así, nuestro intervalo de confianza (así se llama en estadística) será :
nos está diciendo entre que dos valores caerá nuestro valor a estimar con una probabilidad (con una confianza) del 95% (probabilidad (1−?)% para un caso general). Existe otro enfoque para resolver esto, la estadística Bayesiana, cuyo enfoque se pregunta cuál es la probabilidad de que el número de tanques/taxis sea igual a cierto valor. ¿Problema? La estadística Bayesiana parte de una hipótesis inicial subjetiva. Dicho enfoque no se ha explicado en este artículo por dos motivos. Primero, por su complejidad matemática. Y segundo, porque no soy partidario de dicha filosofía. Si estás interesado en la solución Bayesiana al problema, te recomiendo leer la referencia [1].
Enlaces:
https://www.statisticshowto.datasciencecentral.com/german-tank-problem/
https://www.theguardian.com/world/2006/jul/20/secondworldwar.tvandradio
https://www.theguardian.com/technology/blog/2008/oct/08/iphone.apple
https://www.eitb.eus/es/divulgacion/videos/detalle/5465836/video-charla-juan-antonio-cuesta-dia-pi/
Bibliografía:
[1] Höhle, M. and Held, L. (2006). Bayesian estimation of the size of a population. Technical Report SFB 386, No. 399, Department of Statistics, University of Munich.
[2] Johnson, Roger (1994). Estimating the size of a population. Teaching Statistics, 16, 50—52.
[3] Ruggles, R. and Brodie, H. (1947). An empirical approach to economic intelligence in World War II. Journal of the American Statistical Association, 42, 72–91.